Среднее квадратическое

Предлагаемая здесь программа, помимо расчета среднего квадратического, умеет еще и приводить исходные данные к стандартному виду, а так же упорядочивать их по возрастанию или убыванию...

Содержание:

• Определение среднего квадратического
• Свойства среднего квадратического
• Расчет среднего квадратического
• Прикладное значение среднего квадратического

 

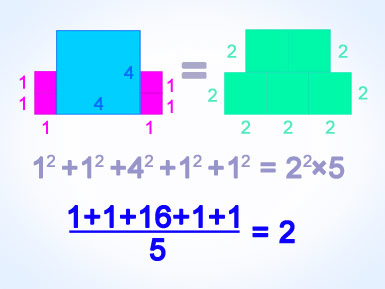Среднее квадратическое, как правило, используется тогда, когда смысловое значение имеет квадрат от значений исходной последовательности.
Рассмотрим такую задачу:
Из конверта выпало 2 квадратика со стороной 1 см, затем большой квадратик со стороной 4 см и еще 2 односантиметровых - всего 5 квадратиков.
Какова должна быть сторона у 5 одинаковых квадратиков, занимающих ту же площадь (рисунок на заставке)?
Если предположить, что это будет средняя длина сторон исходных квадратиков

(1+1+4+1+1)/5 = 1,6

то сильно ошибемся: S_{общ ср дл} = (1,6)² × 5 = 12,8.
В то время как

S_{общ кв} = (1)²+(1)²+(4)²+(1)²+(1)²=20; 20 > 12,8

Значит длина стороны одинаковых квадратиков должна быть равна корню квадратному из S_{общ кв}/5, то есть (20/5)^1/2 = (4)^1/2 = 2 (см) - эта длина и есть среднее квадратическое от сторон квадратов!
Прежде чем начать онлайн расчеты будет уместно вспомнить строгое определение предмета счета:

Среднее квадратическое значение множества заданных чисел определяется как число равное квадратному корню от суммы квадратов этих чисел, делённой на их количество:

 

 

Можно сказать, что среднее квадратическое равно квадратному корню из среднего арифметического^[1] квадратов заданных чисел a₁+ a₂+ …+ a_n и является частным случаем среднего степенного^[2].

Свойства среднего квадратического

1. Среднее квадратическое значение множества заданных неотрицательных чисел лежит между минимальным и максимальным числами из этого множества.

2. Кроме того среднее квадратическое подчиняется неравенству о средних, то есть для любого множества чисел оно не меньше среднего арифметического:

 

Расчет среднего квадратического

Для начала расчета введите исходные числа в одно из полей ввода-вывода данных.
В первое поле можно ввести последовательность чисел, разделенных точкой с запятой (программа попытается так же преобразовать к стандартному виду, например, вставленную копию последовательности чисел с плавающей точкой, разделенных пробелами, запятой или точкой с запятой).
Во второе поле можно вводить числа по одному - они автоматически будут добавляться к данным первого поля, если расчет не запустился автоматически, кликните по зеленой кнопке, показывающей количество чисел в исследуемом массиве:
 

 

ВНИМАНИЕ! При перезагрузке страницы введенная информация не сохраняется, если Вы не сгенерировали код для записи результатов работы в командной строке:

Сохранить расчет среднего квадратического в истории браузера

Адресную строку с кодом из Ваших данных Вы можете можете переслать на любое устройство и воспроизвести на нем результаты расчетов

После того как будут введены хотя бы два исходных числа цвет квадратной кнопки на поле ввода данных должен поменяться с оранжевого на зеленый и автоматически начнется расчет среднего квадратического и сопутствующих параметров, если это не произошло, то кликните по зеленому полю кнопки.

 

Прикладное значение среднего квадратического

Среднее квадратическое от отклонений значений исследуемых данных находит широкое прикладное применение в метрологии и статистике. При обработке результатов измерений во многих случаях их окончательные значения определяются как среднее арифметическое от значений, полученных в результате эксперимента, при этом среднеквадратическое отклонение^[3],[4] величин будет являться оценкой ошибки измерений.
В свою очередь на основе минимизации среднеквадратических отклонений в 19 веке был разработан метод наименьших квадратов, который нашел широкое применение в таких областях как статистический, регрессионный анализ, обработка экспериментальных данных и вычислительная математика.

 

P.S. На этой странице используется Бета версия программы расчета среднего квадратического, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).

 

1. Среднее арифметическое значение (чаще используется термин, просто, "среднее арифметическое" или "среднее") множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:

 

2. Среднее степенное значение   s_d  порядка (степени) d от множества заданных чисел a₁+ a₂+ …+ a_n определяется формулой:

 

Среднее арифметическое является степенным средним c d = 1, среднее квадратическое - d = 2, среднее гармоническое можно считать степенным средним порядка d = -1.

3. Если вычислено арифметическое среднее заданного множества чисел, то во многих случаях, становится желательной оценка рассеяния значений этих чисел относительно среднего. Оценка расходимости квадратов значений этих чисел от среднего и является оценкой дисперсии.
Вообще термин дисперсия появился в рамках теорий вероятностей. Одной из ее основополагающих характеристик является дисперсия случайной величины как мера разброса значений случайной величины относительно её математического ожидания.
Не углубляясь в дебри Тер-Вера, здесь приводим только используемую для наших расчетов формулу дисперсии:

 

4. Среднеквадратическое отклонение σ вычисляется как корень квадратный от дисперсий и возвращает нас в область сопоставимых со средним арифметическим величин:

 

● Главная ▸ Статьи ▸ Блог ▸ Копилка ✔ Среднее квадратическое